x星球的居民脾气不太好，但好在他们生气的时候唯一的异常举动是：摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试，并且评定出一个耐摔指数来，之后才允许上市流通。

x星球有很多高耸入云的高塔，刚好可以用来做耐摔测试。塔的每一层高度都是一样的，与地球上稍有不同的是，他们的第一层不是地面，而是相当于我们的2楼。

如果手机从第7层扔下去没摔坏，但第8层摔坏了，则手机耐摔指数=7。
特别地，如果手机从第1层扔下去就坏了，则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏，则耐摔指数=n

为了减少测试次数，从每个厂家抽样3部手机参加测试。

某次测试的塔高为1000层，如果我们总是采用最佳策略，在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢？

请填写这个最多测试次数。

注意：需要填写的是一个整数，不要填写任何多余内容。

Given an integer with no more than 9 digits, you are supposed to read it in the traditional Chinese way. Output Fu first if it is negative. For example, -123456789 is read as Fu yi Yi er Qian san Bai si Shi wu Wan liu Qian qi Bai ba Shi jiu. Note: zero (ling) must be handled correctly according to the Chinese tradition. For example, 100800 is yi Shi Wan ling ba Bai.

A long-distance telephone company charges its customers by the following rules:

Making a long-distance call costs a certain amount per minute, depending on the time of day when the call is made. When a customer starts connecting a long-distance call, the time will be recorded, and so will be the time when the customer hangs up the phone. Every calendar month, a bill is sent to the customer for each minute called (at a rate determined by the time of day). Your job is to prepare the bills for each month, given a set of phone call records.

One important factor to identify acute stroke (急性脑卒中) is the volume of the stroke core. Given the results of image analysis in which the core regions are identified in each MRI slice, your job is to calculate the volume of the stroke core.

Given a constant $K$ and a singly linked list L, you are supposed to reverse the links of every $K$ elements on $L$. For example, given L being 1→2→3→4→5→6, if $K=3$, then you must output 3→2→1→6→5→4; if $K=4$, you must output 4→3→2→1→5→6.

Stack is one of the most fundamental data structures, which is based on the principle of Last In First Out (LIFO). The basic operations include Push (inserting an element onto the top position) and Pop (deleting the top element). Now you are supposed to implement a stack with an extra operation: PeekMedian – return the median value of all the elements in the stack. With $N$ elements, the median value is defined to be the $(N/2)$-th smallest element if $N$ is even, or $((N+1)/2)$-th if $N$ is odd.

Zhejiang University has 40,000 students and provides 2,500 courses. Now given the registered course list of each student, you are supposed to output the student name lists of all the courses.

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

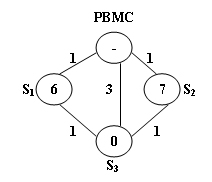
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at $S_3$, we have 2 different shortest paths:

1. PBMC -> $S_1$ -> $S_3$. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from $S_1$ and then take 5 bikes to $S_​3$, so that both stations will be in perfect conditions.
2. PBMC -> $S_2$ -> $S_3$. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.