There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

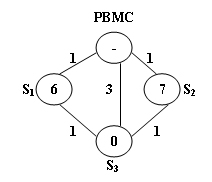
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at $S_3$, we have 2 different shortest paths:

1. PBMC -> $S_1$ -> $S_3$. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from $S_1$ and then take 5 bikes to $S_​3$, so that both stations will be in perfect conditions.
2. PBMC -> $S_2$ -> $S_3$. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.