PAT-A 1099 Build A Binary Search Tree (30)

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.

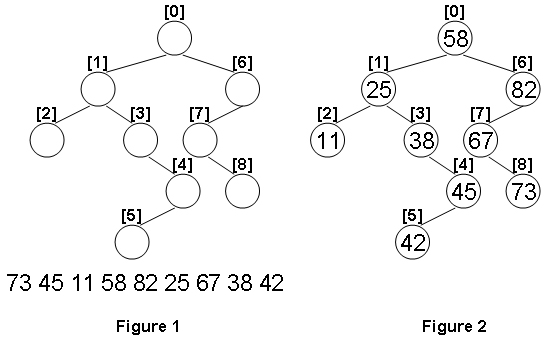
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

Problem: PAT-A 1099 Build A Binary Search Tree

Input Specification

Each input file contains one test case. For each case, the first line gives a positive integer N (≤100) which is the total number of nodes in the tree. The next N lines each contains the left and the right children of a node in the format left_index right_index, provided that the nodes are numbered from 0 to N−1, and 0 is always the root. If one child is missing, then −1 will represent the NULL child pointer. Finally N distinct integer keys are given in the last line.

Output Specification

For each test case, print in one line the level order traversal sequence of that tree. All the numbers must be separated by a space, with no extra space at the end of the line.

Sample Input

1
2
3
4
5
6
7
8
9
10
11

9
1 6
2 3
-1 -1
-1 4
5 -1
-1 -1
7 -1
-1 8
-1 -1
73 45 11 58 82 25 67 38 42

Sample Output

1

58 25 82 11 38 67 45 73 42

Analysis

  题目大意：给一个二分搜索树的结构，和一个数字序列。将数字填入二分搜索树，即对于每个结点，左子树的结点小于父结点，右子树的结点大于等于父结点，左右子树也要满足二分搜索树的条件。最后按层次遍历输出序列。

  由于中序遍历二分搜索树的序列是从小到大排列的，因此首先将序列从小到大排序，然后按照中序遍历将数字从小到大填入二分搜索树。不需要真的填，直接按层号保存数据，最后按层次顺序输出序列。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

#include <bits/stdc++.h>
using namespace std;

int G[105][2], mxL = -1;
vector<int> nod(105), LYR[105];

void build_tree(int root, int lyr, int& idx) {
    mxL = max(mxL, lyr);
    if (G[root][0] != -1) build_tree(G[root][0], lyr + 1, idx);
    LYR[lyr].push_back(nod[idx++]);
    if (G[root][1] != -1) build_tree(G[root][1], lyr + 1, idx);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    int N, l, r;
    cin >> N;
    for (int i = 0; i < N; i++) {
        cin >> l >> r;
        G[i][0] = l, G[i][1] = r;
    }
    for (int i = 0; i < N; i++) {
        cin >> nod[i];
    }
    sort(nod.begin(), nod.begin() + N);
    int idx = 0, flag = 0;
    build_tree(0, 0, idx);
    for (int i = 0; i <= mxL; i++) {
        int len = LYR[i].size();
        for (int j = 0; j < len; j++) {
            if (flag++) cout << " ";
            cout << LYR[i][j];
        }
    }
}

Tsukkomi

  希望考试的时候 30 分的题也出这种……