剪枝策略:采摘当前草药导致超时,或当前结点上界小于已知最优值时剪枝。
在算法分析课上第一次接触分支限界法(Branch & Bound),实验要求使用分支限界法解决 0/1 背包问题。虽然很清楚代码量要远高于 DP,但报告是还要写的,硬着头皮怼吧。随便在蓝桥杯题库找了一道 0/1 背包的基础题做测试,题目是算法训练的 ALGO-30 入学考试。
题目
问题描述
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
第一行有两个整数T(1 <= T <= 1000)和M(1 <= M <= 100),用一个空格隔开,T 代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个在 1 到 100 之间(包括1和100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
样例输入
1 | 70 3 |
样例输出
1 | 3 |
数据规模和约定
对于30%的数据,M <= 10;
对于全部的数据,M <= 100。
解题思想
分支限界法概述
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
对于0/1背包问题来说,就是每访问一个结点,生成两个儿子结点,一个是放入物品,一个是舍弃物品。在生成结点的同时判断该结点是否为可行解,并同时计算该结点下的上界。对于不可行解直接剪枝,可行结点使用优先队列存储。不断扩展队列优先级最高的结点,也就是上界最大的结点,当优先队列中优先级最高的结点上界不大于已知的值时,循环结束,当前得到的最优值即为所求最优值。
具体思路
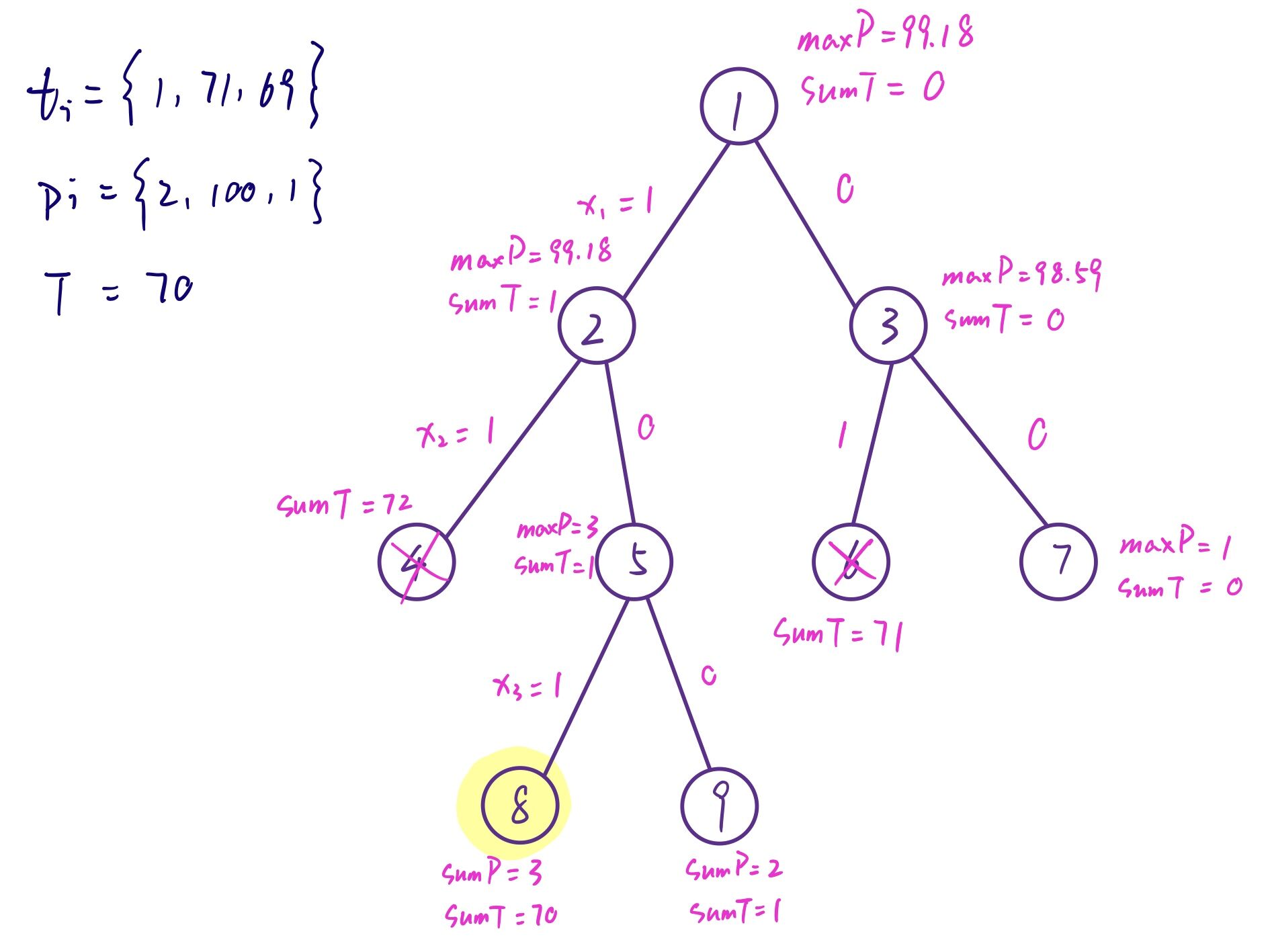
放到本题来看,每个草药包括两个属性:采集时间和价值。首先将所有草药按单位时间的价值从高到低排序,使用二叉树构造解空间树,每层结点代表正在放置第几个草药。由此,每个结点将能够扩展两个子节点,即放入 N 号草药和不放入 N 号草药。分别为每个扩展的结点计算上界,即计算规定时间内可拆分条件下的最大价值。如果当前结点的时间超出给定总时间 T 或者上界小于当前已知最优值,则剪枝处理,其余放入优先队列。
设定优先队列为大顶堆的数据结构,不断从优先队列中取出优先级最高(上界大于已知最优值)的结点,对其扩展。如果该结点已扩展至叶结点(所在路径已遍历所有草药),则与当前已知最优值比较,取最大值。当队列中所有结点的上界均不大于当前已知最优值时,循环结束。计算过程和解空间树如下图。
AC代码
1 |
|
扯淡
纯按自己的理解写的,所以不清楚代码是否规范。交上去顺利 AC 了,起初数据量较大的两个测试用例用了 15ms,后来稍微优化下全部 0ms 通过了。代码量有点大,不过效率比想象要高,其实还是 DP 效果好。算法思想是跟着油管的印度大叔 Abdul Bari 学的。视频地址:0/1 Knapsack using Branch and Bound

