The lowest common ancestor (LCA) of two nodes U and V in a tree is the deepest node that has both U and V as descendants.

Given any two nodes in a binary tree, you are supposed to find their LCA.

A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
• Both the left and right subtrees must also be binary search trees.

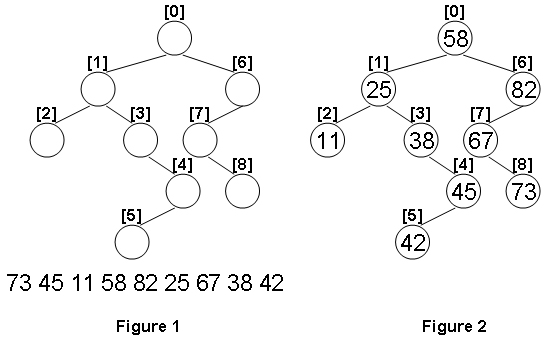
Given the structure of a binary tree and a sequence of distinct integer keys, there is only one way to fill these keys into the tree so that the resulting tree satisfies the definition of a BST. You are supposed to output the level order traversal sequence of that tree. The sample is illustrated by Figure 1 and 2.

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

Given a singly linked list, you are supposed to rearrange its elements so that all the negative values appear before all of the non-negatives, and all the values in [0, K] appear before all those greater than K. The order of the elements inside each class must not be changed. For example, given the list being 18 → 7 → -4 → 0 → 5 → -6 → 10 → 11 → -2 and K being 10, you must output -4 → -6 → -2 → 7 → 0 → 5 → 10 → 18 → 11.

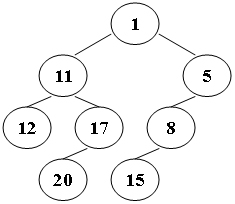
Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences. And it is a simple standard routine to print the numbers in level-order. However, if you think the problem is too simple, then you are too naive. This time you are supposed to print the numbers in “zigzagging order” – that is, starting from the root, print the numbers level-by-level, alternating between left to right and right to left. For example, for the following tree you must output: 1 11 5 8 17 12 20 15.

Given a singly linked list L with integer keys, you are supposed to remove the nodes with duplicated absolute values of the keys. That is, for each value K, only the first node of which the value or absolute value of its key equals K will be kept. At the mean time, all the removed nodes must be kept in a separate list. For example, given L being 21 → -15 → -15 → -7 → 15, you must output 21 → -15 → -7, and the removed list -15 → 15.

Mice and Rice is the name of a programming contest in which each programmer must write a piece of code to control the movements of a mouse in a given map. The goal of each mouse is to eat as much rice as possible in order to become a FatMouse.

First the playing order is randomly decided for $N_P$ programmers. Then every $N​_G$ programmers are grouped in a match. The fattest mouse in a group wins and enters the next turn. All the losers in this turn are ranked the same. Every NG winners are then grouped in the next match until a final winner is determined.

For the sake of simplicity, assume that the weight of each mouse is fixed once the programmer submits his/her code. Given the weights of all the mice and the initial playing order, you are supposed to output the ranks for the programmers.

Given an increasing sequence S of N integers, the median is the number at the middle position. For example, the median of $S_1$ = { 11, 12, 13, 14 } is 12, and the median of $S_2$ = { 9, 10, 15, 16, 17 } is 15. The median of two sequences is defined to be the median of the nondecreasing sequence which contains all the elements of both sequences. For example, the median of $S_1$ and $S_2$ is 13.

Given two increasing sequences of integers, you are asked to find their median.

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.

Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 110 be true? The answer is yes, if 6 is a decimal number and 110 is a binary number.

Now for any pair of positive integers $N_1$ and $N_2$, your task is to find the radix of one number while that of the other is given.